水（和溶解空气）的可压缩性导致水的作用不同于金属柱。如果它不可压缩，其前缘将被永久压碎，或者整个色谱柱将向后弹回。当水柱的前缘碰到关闭的阀门时，它突然停止。由于前缘后面的水仍在运动，因此开始压缩。即使前缘已停止，这也允许少量水继续流入管道。当流动停止时，其所有运动动能以及由于压缩而产生的动能都转换为压力能。
压缩从水柱的前缘开始，由于它产生的额外能量无法继续通过关闭的阀门，因此会产生压力或冲击波，并沿着阻力最小的路径传播，在此示例中，该路径返回上游。它的开始类似于在空气中传播的声波撞击类似的屏障时产生的回声。当波撞击上游阀门时，它将被反射回下游，但强度减弱。这种来回运动一直持续到摩擦和反射损耗导致波消失为止。波浪传播的速度及其在传播过程中损失的能量取决于其传播介质的密度和可压缩性。水的密度和可压缩性使其成为冲击波产生和传播的良好介质。
由液压冲击产生的压力波具有与声波相似的特性，并且以相似的速度传播。水锤压力波协商管道长度所需的时间就是管道长度除以水中的声速（大约4,860英尺每秒[ft / sec]）。在水锤分析中，经常使用的时间常数描述了波从开始到次要屏障然后再返回的过程。它的形式为Tc = 2L / a（其中L是管道长度，a是波速，即声速）。在1,000英尺长的管道中，波浪可以在不到半秒的时间内完成一次完整的往返。
P（附加）= aV / 2.31g
公式1
P =冲击波产生的附加压力
a =波速
V =管中流动的水的速度，以英尺/秒为
单位g =万有引力常数32 ft / sec 2
2.31 =压力转换常数。
该冲击波产生的压力与波速和管道中流动的水速都成正比。尽管公式1没有考虑管长度，直径和弹性的影响，但它将为水锤压力波产生的附加压力提供一些见识。
在5英尺/秒的管道速度下，由冲击波产生的附加压力约为328 psi。将该速度增加到10 ft / sec，将附加压力增加到大约657 psi。显然，未设计为适应这种增加的压力的系统经常会损坏甚至毁坏。
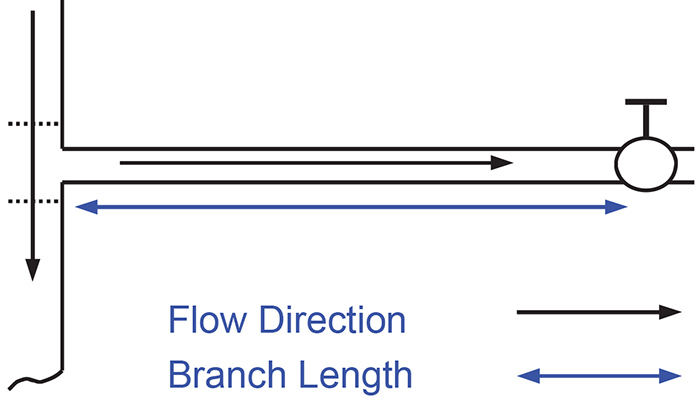图2.带有分支电路的主管道
阀门关闭与开启
水锤的主要原因之一是阀门突然关闭。图2显示了带有“三通”馈送支路的主管道。在支路的末端是一个阀门。黑色箭头表示主管线和分支管线中的流向，紫色箭头表示分支管线的长度。与图1中的系统一样，阀门充当主要屏障，但这次的次要屏障是“三通”。
如果水在支管中流动且阀门迅速关闭，则会产生冲击波。在我们的假设示例中，它的开始遵循相同的事件顺序。一个小区别是，由于“ Tee”通向两侧的主管道，因此某些波的强度会丢失。尽管如此，仍有很大一部分会反射回阀。
P = 0.07（VL / t）
公式2
P =冲击波产生的附加压力
V =流速（以英尺/秒为单位）
L =挡板之间的管道长度（以英尺为单位）
t =阀门关闭时间（以秒为单位）。
0.07 =导出常数。
此示例的不同之处在于，我们可以对阀门关闭时间进行一些控制。在我们的假设示例中，阀门以接近光速的速度关闭。闭合时间对水锤的产生和强度有重要影响。其他两个变量，流速和管道长度也是主要因素。公式2显示了这三个变量的关系。冲击波产生的附加压力与流速和管道长度成正比，与关闭时间成反比。换句话说，较高的V或L值将增加压力，而较高的t值将导致压力降低。表1显示了使用不同的速度，管道长度和关闭时间时，该方程式的结果。V值为5和10英尺/秒，L值为100和1,000英尺，和t值为1和2秒。每个示例中有两个变量是常量。
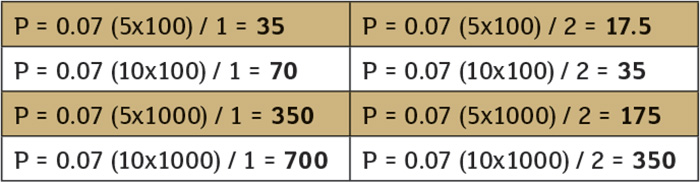表1.不同速度，管道长度和关闭时间所产生的附加压力
该表的两列都说明了速度和长度的比例影响-压力随着它们的增加而增加。右栏中的较低值说明了时间的反比关系。这些压力是左栏中的一半，因为关闭时间增加了一倍。L的值通常是固定的，并取决于应用程序，但是我们可以对其他两个变量进行实质控制。通过这样做，我们可以消除或大大降低水锤效应。
管道直径及其材料的弹性也会影响所产生的压力。更大直径和更多弹性的材料吸收了一些冲击波的强度，因此降低了产生的压力。几家管道制造商发布了曲线或表格，显示了各种直径和材料的水锤潜在的压力增加。
假设分支管路阀已关闭。如果快速打开，其效果类似于快速关闭的效果。当阀门快速打开时，支管会立即出现压力下降，而来自主管的进水会加速以前的静态塔。由于摩擦和其他因素限制了其流动，因此色谱柱的前部可作为初始屏障并引起水击。通常，其影响远小于阀门关闭的影响，通常被称为“喘振”。不过，在某些情况下，这种喘振可能会造成破坏。